简易语音辨识原理初探
简易语音辨识原理初探
很久没有写博客了,最近博客还因为各种原因故障了,反正现在修好了,不管了凑合用吧。最近学习了语音识别相关的一些知识,就在这里简单记录以下学习过程吧。
流程简介
识别任何一个东西流程基本都是先获取这个东西的特征,之后再根据它的特征来判断这个东西的类别,语音识别也不例外。整个识别过程首先进行语音信号的采集,采集到语音信号之后获取信号的mfcc(Mel频率倒谱系数)参数,也就是语音信号的特征。随后采集到特征之后与和预先存入的语音模板进行匹配,也就是根据特征判断类别,匹配过程使用dtw(动态时间归整)算法。整个方案流程图如下:
1 | st=>start: 开始 |
其实核心就两部分
- mfcc参数提取
- dtw模板匹配
mfcc参数提取
我们现在知道了语音识别的第一步是获取到语音信号的特征,好在科学家们已经为我们找到一种很好描述语音特征的方法,于是就引出了mfcc这样一种可以描述不同语言特征的东西。mfcc(Mel Frequency Cepstral Coefficents) 翻译过来就是 梅尔频率倒谱系数。那么这是个啥,根据名字我想把它拆分成两部分,即梅尔频率和倒谱系数。
倒谱系数是什么
倒谱是什么这个概念可能大家没有听说过,但学习过信号与系统都应该知道频谱是什么。首先我们来看一个频谱:

图为数字”0”的短时傅里叶变换的频谱。这里又引入了一个概念叫短时傅里叶变换,它的意思是将一段长时间(比如2s)的语音信号进行拆分成一帧一帧的短时信号(这里使用的25ms),再计算这一帧语音信号的频谱。长时间的傅里叶变换出来的频谱不同语言差异不大,毕竟时间一长数据一多就一不小心依概率收敛到一个差不多的频谱范围了,这样就没办法提取特征。只有短时间的频谱才有明显的差异,并且结合帧与帧之间的变化情况才能更好的获取特征。
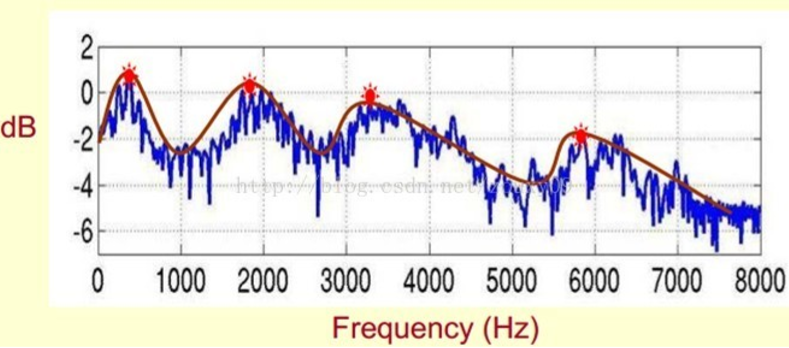
此外,观察这张频谱图可以发现在特定位置有一些峰,并且这些峰之间的间隔还差不太多,也就是说这些峰有特定的频率分量。到这里就引入了频谱的频谱的概念,离我们想要的倒谱的距离越来越近了哈。在这里我们把这些峰叫做共振峰,由一个声音的基频和它的高次谐波的叠加,也正是因为谐波分量的幅值不同,从而产生了各种各样的音色。由于共振峰在频谱上十分明显,我们就想到把他提取出来,通过检测帧与帧之间共振峰的变化情况不就能找到一个语音的特征了吗? 我们要提取的不仅仅是共振峰的位置,还得提取它们转变的过程。所 以我们提取的是频谱的包络。这包络就是一条连接这些共振峰点的平滑曲线。
那么我们如何提取这条曲线?我们可以将这条复杂的曲线分成两部分,包络和细节。从而可以写出表达式:$曲线=包络\times细节$,通过对曲线求对数就可以得到新的表达式:$\log(曲线)=\log(包络)+\log(细节)$好了这样我们就把一个乘性信号变成了一个加性信号。对这个加性信号做傅里叶变换再取它的低频分量,我们就成功的获取到了包络的频率,也就是共振峰的频率。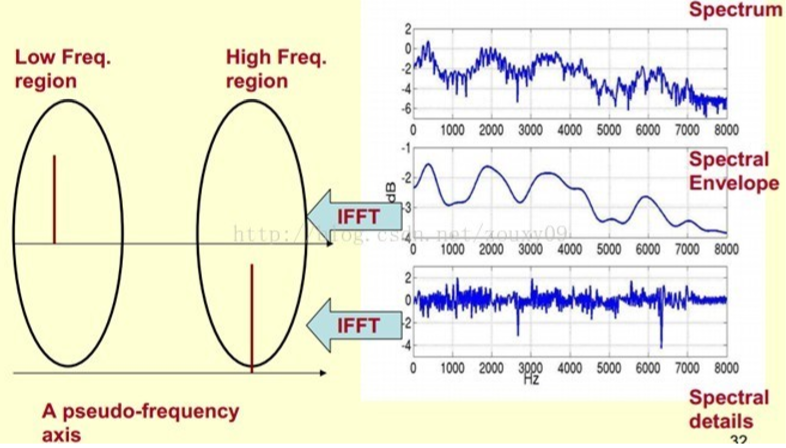
好了到目前为止,我们获取到的这个频谱就被称之为 倒谱 它把乘性信号分离成了加性信号,而这整个过程我们称之为同态滤波。因为,做了两次fft得到了频域的频域,从另一个角度来说两次fft又相当与变换到了时域,所以输入输出信号都是时域,所以是同态。
由于我们只关系共振峰,也就是倒谱的低频分量,所以我们通常来说只取倒谱的前13个参数即可。最后再总结一遍流程:
1 | time=>inputoutput: 乘性时域信号 |
$x(n)=x_1(n)\ast x_2(n) \longrightarrow \hat x(n)=\hat x_1(n)+ \hat x_2(n)$
梅尔频率是什么
到这里我们又涉及到了另一个关键词–梅尔频率(Mel-Frequency)。对于人类听觉感知的实验表明,人类听觉的感知只聚焦在某些特定的区域,而不是整个频谱包络。人的听觉系统是一个特殊的非线性系统,它响应不同频率信号的灵敏度是不同的。在语音特征的提取上,人类听觉系统做 得非常好,它不仅能提取出语义信息, 而且能提取出说话人的个人特征,这些都是现有的语音识别系统所望尘莫及的。如果在语音识别系统中能模拟人类听觉感知处理特点,就有可能提高语音的识别率。在Mel频域内,人对音调的感知度为线性关系。举例来说,如果两段语音的Mel频率相差两倍,则人耳听起来两者的音调也相差两倍。
综上得出两点结论:
- 人耳频率非线性
- 人耳对某些频率分量不敏感
所以为了更好的模拟人耳,我们需要对声音信号做一些处理,对于非线性问题我们用梅尔频率来解决,对于不敏感问题我们就用带通滤波器组来解决,结合起来我们就有了梅尔滤波器组。
流程图如下:
1 | in=>inputoutput: 输入信号 |
Mel频率的公式如下:$$ Mel(f)=2595\times\lg(1+\frac{f}{700})$$
或者$$Mel(f)=1125\times\ln(1+\frac{f}{700})$$
Mel带通滤波器公式如下:
$$H_m(k)=\begin{cases}
0 & k<f(m-1) \\
\frac{2(k-f(m-1))}{(f(m+1)-f(m-1))(f(m)-f(m-1))} & f(m-1) \leq k\leq f(m) \\
\frac{2(f(m+1)-k)}{(f(m+1)-f(m-1))(f(m)-f(m-1))} & f(m) \leq k\leq f(m+1) \\
0& k \geq f(m+1)
\end{cases}$$
Mel滤波器在hz频率如图所示:
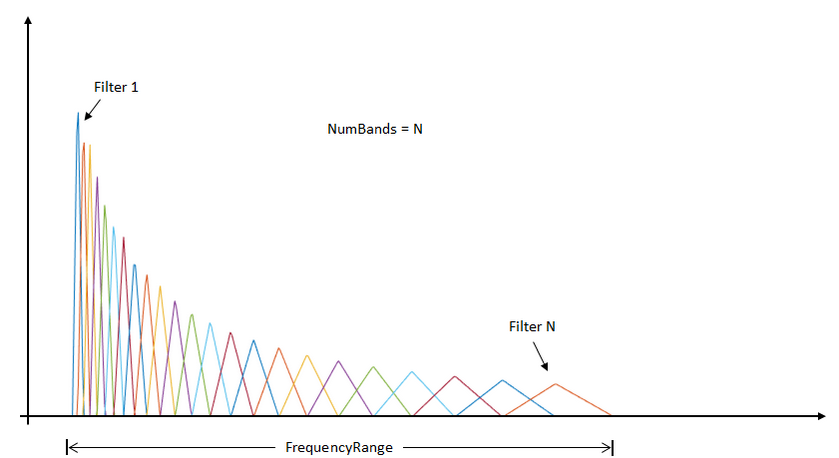
##完整的mfcc参数提取过程
说了这么多,最终结合起来流程图就是:
1 | time=>inputoutput: 乘性时域信号 |
需要说明的是人说话高频分量往往不是很大,但是为了抓取特征就需要增强高频分量,即预加重。另外分帧之后加窗有利于帧间信号平稳过渡。最终得到的应该是一个长宽分别为mfcc参数维度(一般取13维)和帧个数的矩阵。
mfcc参数提取部分python代码如下
1 | import numpy |
DTW算法模板匹配
DTW算法即动态时间规整算法。对于语音识别我们很简单的想法就是逐帧计算输入信号和模板之间的欧式距离,之后再将每一帧的距离相加求得一个总的距离,如果距离小于某个阈值我们就能认为这两个信号很相似,就匹配成功。依次匹配多个模板,找到距离最短的模板就能识别一些关键字了。
$$ 总距离=\sum^{所有的帧}_{i}{\sqrt{\sum_j^{维度}(模板_j-信号_j)^2}}$$
但是! 想法虽然简单,不过考虑到人说话的快慢问题和语音信号长短问题,这样计算相似度往往不是很准确,甚至不同长度的信号根本无法计算相似度。比如下图所示信号,相似程度很高但是按照上面的算法却无法计算出来正确的相似度,而通过虚线对应关系计算出来的相似度才是正确的相似度。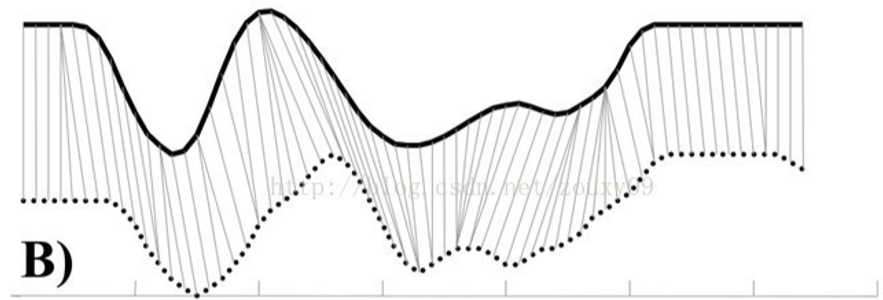
通过将一个信号扭曲之后再和另一个信号计算相似程度就能解决问题。并且这里的信号扭曲也只能是局部的平移伸长或者缩短,但不能出现局部信号反转的情况。
那么怎样将信号扭曲呢。我们不妨假设信号$\vec a$长度为6,信号$\vec b$长度为4,逐个计算$\vec a$中每个元素和$\vec b$中每个元素的欧式距离,我们就能得到一个$6\times 4$的矩阵,如下所示: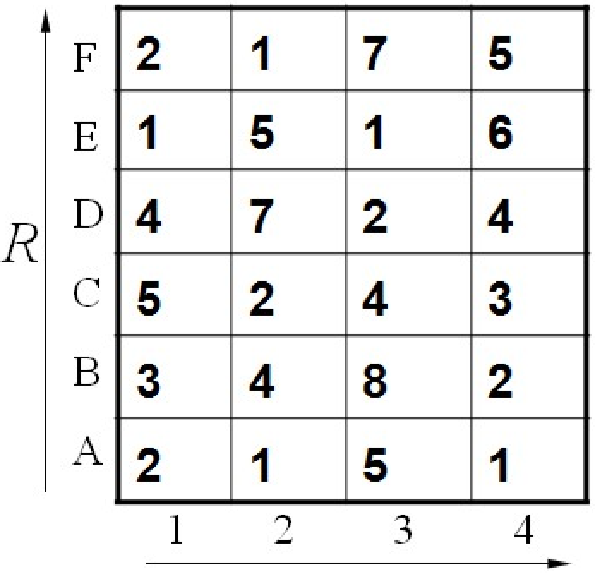
其中[A,1]点代表$\vec a[1]$和$\vec b[1]$的距离,[D,3]点代表$\vec a[5]$和$\vec b[3]$的距离以此类推。左下角代表两个信号的起始点,右上角代表两个信号的终点。因为信号是在局部可以扭曲的,所以我们寻找最短距离就在某个点的邻域内寻找最短的距离。但又因为局部信号不能反转,所以我们只需要在某个点的上方,右方和右上方寻找最短距离即可。比如[C,2]点的下一个点的距离分别是7,4,2,这里我们取最小点2。从起始点依次求最短路径后就能得到一条蜿蜒的曲线,将这条曲线上左右的距离加起来就能得到总最短路径,也就是两个信号的相似程度。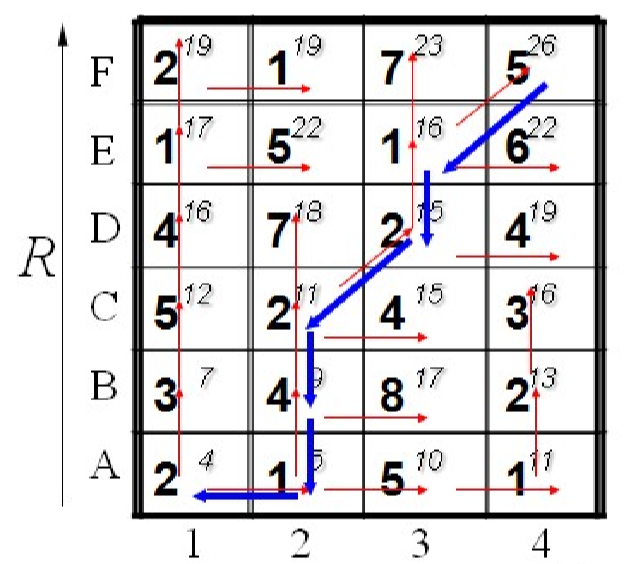
当然了直接这样找距离会存在一些问题。因为这个找出来的距离高度依赖起始点的位置,但是如果这个两个信号相似的起始点不在一起这样找出来的距离不就不正确了吗?更好的方法是找出终点后再回溯回来,不过这样略微复杂,而且我发现不回溯其实识别效果也不错,所以我也没有进一步研究。
到目前为止我们就获得了两个信号之间的距离,多次进行模板匹配再取最小距离就能识别特定的关键字啦。
DTW模板匹配部分python代码如下
1 | from mfcc import mfcc |
工程源码
工程源码可以从本站下载:https://github.com/ZzzzzzS/Numbervoicerecognition/releases/tag/V1.0
需要的包:numpy,scipy,pyaudio,PySide2等。
总结
写到这里我已经没什么好说的了,但是还是要假装有个总结,来证明我又学到了什么新的东西。。。
思考了很久确实不知道写啥了,就这样吧,the end!
参考文献
- 胡航.语音信号处理.哈尔滨工业大学出版社,2009.7
- 周志权等.数字信号处理.哈尔滨工业大学出版社,2012.12
- 张学工.模式识别(第三版).清华大学出版社,2010.8
- 金大(臣尔).Qt5开发实战.人民邮电出版社,2015.9
- IT-Sunshine.动态规划DTW算法的实现,
https://blog.csdn.net/weixin_39338645/article/details/84063108 - Zouxy09.语音信号处理之(四)梅尔频率倒谱系数(MFCC),
https://blog.csdn.net/zouxy09/article/details/9156785








