简易图像拼接原理初探
简易图像拼接原理初探
今天突然高产,一天写了两篇博客,可能是博客修好之后有些激动吧。废话不多说,进入正题图像拼接。
首先放一张效果图:

这张图是两张图拼接而成,看看能找到拼接缝吗
图像拼接整体思路
整个图像拼接过程首先读入图像后使用fast检测算法识别图像中的特征点,然后计算特征点的向量获取到一个128位长的向量,随后通过对所有向量的逐个匹配计算出匹配的特征点并挑选出距离最短的前N个点作为最佳匹配点,以上识别过程就结束。接下来进行拼接过程,通过计算最佳匹配点可以获取到仿射变换矩阵,利用仿射变换矩阵可以计算出仿射变换后图像的顶点以及图像本身。之后将仿射变换后的图像和另一张待拼接的图像拼接起来即可,拼接后的拼接缝处理利用重叠区域加权平均的思想来处理。以下是整个图像拼接的流程图:
1 | st=>start: 开始 |
FAST算法提取特征点
FAST的提出者Rosten等将FAST角点定义为:若某像素与其周围邻域内足够多的像素点相差较大,则该像素可能是角点。
核心思想如下:该算法的基本原理是使用圆周长为16个像素点来判定其圆心像素P是否为角点。在圆周上按顺时针方向从1到16的顺序对圆周像素点进行编号。如果在圆周上有N个连续的像素的亮度都比圆心像素的亮度Ip加上阈值t还要亮,或者比圆心像素的亮度减去阈值还要暗,则圆心像素被称为角点。
详细计算方法如下:
选择某个像素$p$其像素值为$I_p$以$p$为圆心,半径为三个像素确定一个圆,圆上有16个像素点记作$P_1,P_2,P_3\ldots P_{16}$
确定一个阈值记作t
让圆上的n个连续的像素的像素值与p的像素值做差,若这些差值的绝对值都比$I_\sigma+t$大或者都比$I_\sigma-t$小则像素$p$为角点。现在我们令n=12(经验数据)。接下来是实现这一步的具体步骤(前人经验所得)。
分别计算$P_1$与$P_\sigma$的像素值与$I_\sigma$的差,若差值的绝对值都比大$I_\sigma+t$或都比$I_\sigma-t$小,则进入下一步判断,否则P点被丢弃
分别计算$p_1$,$p_2$,$p_3$,$p_4$四个点像素值与$I_\sigma$的差值,若有个点的差值的绝对值都比$I_\sigma+t$大或都比$I_\sigma-t$小,则进入下一步判断,否则$P$点被丢弃
对圆上16个像素点的像素值分别与$I_\sigma$做差,若有n个像素点的差值的绝对值都比$I_\sigma+t$大或都比$I_\sigma-t$小,则$p$点为角点
在OpenCV中利用fast检测子计算特征点的代码如下:
1 | Ptr<FastFeatureDetector> detector = FastFeatureDetector::create(); //fast检测子 |
效果如图所示:

计算特征点的特征向量
在获取到特征点后下一步就需要判断特征点的方向即特征点的向量,为下一步匹配特征点做准备。详细的计算方法如下:
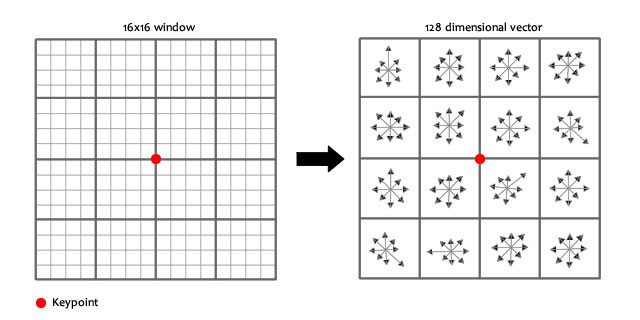
将关键点周围的像素旋转到一个统一的方向,以保证方向不变性。
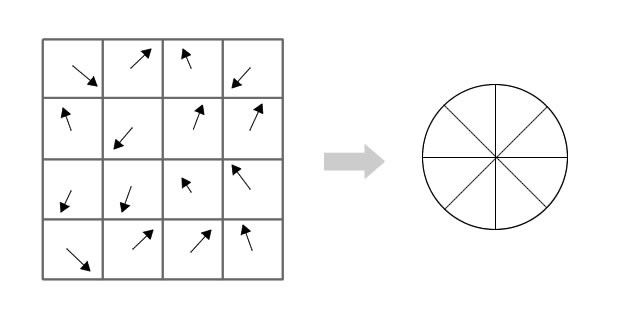
将这些像素分成$4\times4$的小块。
对每个格子进行分析,将格子中的像素计算梯度,映射到8个方向上,对于每一个格子,可以得到一个8维的向量,对于一个关键点周围16个格子,则得到了$16\times8=128$维的向量,这就是一个关键点特征向量。
$$m\left(x,y\right)=\sqrt{\left(L\left(x+1,t\right)-L\left(x-1,y\right)\right)^2+\left(L\left(x,y+1\right)-L\left(x,y-1\right)\right)^2}$$
$$\theta=\alpha tan^2\left(\left(L\left(x,y+1\right)-L\left(x,y-1\right)\right)/\left(L\left(x+1,y\right)-L\left(x-1,y\right)\right)\right)$$
在OpenCV中计算特征点的特征向量的代码如下,由于OpenCV中没有专门针对fast算法的特征向量提取算法,所以我使用了sift算法中的特征向量展开子:
1 | Ptr<SiftDescriptorExtractor> extractor = SiftDescriptorExtractor::create();//展开子 |
特征点的向量如下图所示:

匹配特征点与获取最佳特征点
首先进行特征点的匹配,特征点的匹配使用的BruteForce方法,也就是蛮力匹配器,顾名思义,它的工作原理是:在第一幅图像上选取一个关键点,然后依次与第二幅图像的每个关键点进行(描述符)距离测试,最后返回距离最近的关键点。获取到所有匹配的特征点后计算所有特征点在图像中的距离,并计算距离最短的特征点。之后取出距离在最短距离特征点长度两倍以内(经验数据)的特征点,将这些特征点视为最佳特征点。
在OpenCV中匹配特征点和计算最佳特征点的部分代码如下所示:
1 | Ptr<DescriptorMatcher>matcher=DescriptorMatcher::create(DescriptorMatcher::MatcherType::BRUTEFORCE); //创建暴力匹配器 |
匹配的特征点如下图所示:

计算仿射变换矩阵
仿射变换是几何中的一个概念。仿射变换是一个从实射影平面到射影平面的可逆变换,直线在该变换下仍映射为直线。它是一对透视投影的组合。它描述了当观察者视角改变时,被观察物体的感知位置会发生何种变化。射影变换并不保持大小和角度,但会保持重合关系和交比。对于图像1中的$a\left(x_1,y_1\right)$点和图像2中的$b\left(u_1,v_1\right)$点,通过仿射变换矩阵变换关系如下:$\mathbf{a}=H\mathbf{b}$,其中H就是仿射变换矩阵。由于图像中的变换都是线性变换,所以对图像中的所有点都有以下公式:
$$
\left[\begin{matrix}x\\y\\1\\\end{matrix}\right]=\left[\begin{matrix}h_{00}&h_{01}&h_{02}\\h_{10}&h_{11}&h_{12}\\h_{20}&h_{21}&h_{22}\\\end{matrix}\right]\left[\begin{matrix}u\\v\\1\\\end{matrix}\right]
$$
所以可以通过特征点的匹配关系来找到矩阵H,随后通过矩阵H就能将图像变换到另一幅待拼接图像的平面上。在OpenCV中图像寻找矩阵H使用的是RANSAC算法,即随机抽样一致算法(RANdom SAmple Consensus)。下面介绍RANSAC算法的基本原理:
OpenCV中滤除误匹配对采用RANSAC算法寻找一个最佳单应性矩阵H,矩阵大小为$3\times3$。RANSAC目的是找到最优的参数矩阵使得满足该矩阵的数据点个数最多,通常令$h33=1$来归一化矩阵。由于单应性矩阵有8个未知参数,至少需要8个线性方程求解,对应到点位置信息上,一组点对可以列出两个方程,则至少包含4组匹配点对。RANSAC算法从匹配数据集中随机抽出4个样本并保证这4个样本之间不共线,计算出单应性矩阵,然后利用这个模型测试所有数据,并计算满足这个模型数据点的个数与投影误差(即代价函数),若此模型为最优模型,则对应的代价函数最小。
$$\sum_{i=1}^{n}\left(x_i-\frac{h_{11}u_i+h_{12}v_i+h_{13}}{h_{31}u_i+h_{32}v_i+h_{33}}\right)^2+\left(y_i-\frac{h_{21}v_i+h_{22}v_i+h_{23}}{h_{31}u_i+h_{32}v_i+h_{33}}\right)^2$$
RANSAC算法步骤:
- 随机从数据集中随机抽出4个样本数据 (此4个样本之间不能共线)(包含(x,y)坐标,所以只需要4个点),计算出变换矩阵H,记为模型M
- 计算数据集中所有数据与模型M的投影误差,若误差小于阈值,加入内点集 I
- 如果当前内点集 I 元素个数大于最优内点集 $I_{best}$,则更新$I_{best} = I$,同时更新迭代次数k
- 如果迭代次数大于k,则退出; 否则迭代次数加1,并重复上述步骤
在OpenCV中仿射变换矩阵计算的部分代码如下:
1 | Mat homo = findHomography(imagePoints2, imagePoints1, RANSAC);//计算仿射变换矩阵 |
计算出的矩阵如下:
1 | [0.4186871730549565, -4.990085725145821, 289.5264601465362; |
由于浮点是精度问题可以看出有一定误差
图像顶点计算与图像变换
获取到仿射变换矩阵之后只需要进行仿射变换就能得到所需的图像,由于OpenCV中矩阵无法自由的伸缩大小,所以需要先计算图像的顶点来确定变换后图像的大小,之后再进行图像的变换。由之前的仿射变换公式可以得出顶点的变换公式如下。同理,图像的变换公式也类似:
$$
\left[\begin{matrix}变换后顶点坐标x\\变换后顶点坐标y\\1\\\end{matrix}\right]=\left[\begin{matrix}h_{00}&h_{01}&h_{02}\\h_{10}&h_{11}&h_{12}\\0&0&1\\\end{matrix}\right]\left[\begin{matrix}变换前顶点坐标x\\变换前顶点坐标y\\1\\\end{matrix}\right]
$$
在OpenCV中图像变换和顶点计算的部分代码如下:
1 | //左下角(0,src.rows,1)顶点计算 |
效果如下:

图像拼接与拼接缝处理
到目前为止,将变换后的图像和另一张图像直接拷贝到一个矩阵里即可实现,但是这将导致拼接部分产生接缝。我处理拼接缝的方式是首先计算重叠的区域,在重叠的区域内对两幅图像加权求和。
在OpenCV中拼接与拼接缝处理的部分代码如下:
1 | //进行图像拼接 |
效果如下:

工程源码
整个图像拼接的代码如下:
1 |
|
工程使用OpenCV4.1,Qt5.13,visual studio2019构建。工程下载地址如下:
https://github.com/ZzzzzzS/imagestitch/releases/tag/1.0
总结
这次新学习了OpenCV在图像处理当中的应用。重新复习了C++和Qt相关的基本语法和框架,也体会到了C++语言性能上的优势和OpenCV强大的图像处理能力。
我学习到了很多数字图像处理方面的知识,学习到了很多课本以外的知识。尤其是在特征点检测方面,我了解到了很多很新很先进的算法,比如fast,sift,surf,harris,ORB算法等等。另外在图像变换方面我学习到了透视变换和仿射变换等变换,也加深了对矩阵和图像的理解。
在写这个程序的时候,我遇到了很多很大的困难,但最终都独立一一克服了。由于我使用的是最新版的OpenCV,最新版OpenCV移除了原本的各种检测子而只提供源码编译。所以在OpenCV环境的搭建上遇到了很大的困难。其次由于新版OpenCV修改了很多函数的用法,这导致和网络上的资料有很多不一样的地方,不过这通过一步一步的阅读官方的文档,最终独立写出了整个拼接算法。在克服了重重困难之后,这进一步提高了我的代码能力和对OpenCV的熟悉程度,同时也增强了我独立解决问题的能力。
参考文献
- Rafael C.G.数字图像处理(第三版).电子工业出版社,2017.5
- 金大(臣尔).Qt5开发实战.人民邮电出版社,2015.9
- 胡社教.基于相位相关的全景图像拼接.合肥工业大学学报(自然科学版),2007.1第30卷第1期
- Madcola. OpenCV探索之路(二十三):特征检测和特征匹配方法汇总,https://www.cnblogs.com/skyfsm/p/7401523.html
- Madcola. OpenCV探索之路(二十四)图像拼接和图像融合技术, https://www.cnblogs.com/skyfsm/p/7411961.html
- Open Source Computer Vision.API Online documentation.4.10







